| 
Definición
de lugar geométrico Una
figura es el lugar geométrico de los puntos que cumplen una propiedad cuando:
w Todos los
puntos de la figura cumplen esa propiedad w
Todo punto que cumple la propiedad pertenece a la figura. 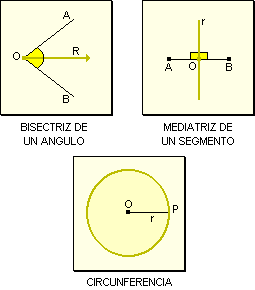

Distancia
de un punto a una recta 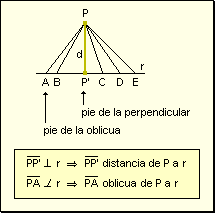
Se
llama distancia de un punto a una recta al segmento de perpendicular comprendido
entre el punto y la recta y cumple las siguientes propiedades:
w Propiedad
1: La distancia de un punto a una recta es
menor a cualquier otro segmento oblicuo comprendido entre ese punto y esa recta. 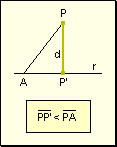
w Propiedad
2: Si dos segmentos oblicuos entre un punto
y una recta tienen sus pies equidistantes del pie de la perpendicular, son congruentes. 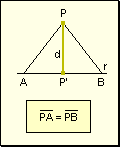
w Propiedad
3: Dados dos segmentos oblicuos entre un
punto y una recta, el menor será aquel cuyo pie se encuentre más
próximo al pie de la perpendicular. 
Las
propiedades recíprocas a las anteriores son:
w Recíproca
1: El menor de los segmentos comprendidos entre un punto y una recta es la
distancia del punto a esa recta. w
Recíproca 2: Si dos segmentos comprendidos entre un punto y una
recta son iguales, sus pies equidistan de la perpendicular trazada entre ese punto
y la recta. w
Recíproca 3: Dados dos segmentos oblicuos entro un punto y una recta,
si el primero es menor que el segundo, el primer pie estará más
cerca del pie de la perpendicular que el segundo pie. 
Propiedad
1 La distancia de un punto a
una recta es menor a cualquier otro segmento oblicuo comprendido entre ese punto
y esa recta. 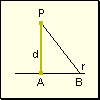
Hipótesis 
Tesis 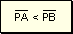
Demostración 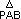 es un triángulo rectángulo donde:
es un triángulo rectángulo donde:
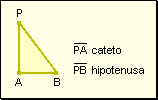
Como
en todo triángulo rectángulo los catetos son menores que la hipotenusa: 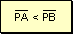
que
es lo que se quería demostrar. 
Propiedad
2 Si dos segmentos oblicuos entre
un punto y una recta tienen sus pies equidistantes del pie de la perpendicular,
son congruentes. 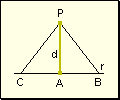
Hipótesis 
Tesis 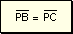
Demostración 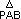 y
y 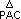 son triángulos
rectángulos donde: son triángulos
rectángulos donde:

De
acuerdo a los criterios de igualdad de triángulos rectángulos: 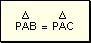
Por
lo tanto: 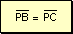
que
es lo que se quería demostrar. 
Propiedad
3 Dados dos segmentos oblicuos
entre un punto y una recta, el menor será aquel cuyo pie se encuentre más
próximo al pie de la perpendicular. 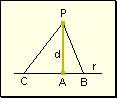
Hipótesis 
Tesis 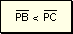
Demostración Para
el triángulo 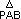 ,
,  es un ángulo
exterior, por lo tanto: es un ángulo
exterior, por lo tanto: 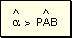 (1)
(1)
Por ser 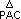 rectángulo:
rectángulo: 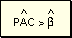 (2)
(2)
De (1) y (2) 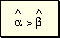
Como
en todo triángulo a mayor ángulo se opone mayor lado: 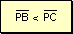
que
es lo que se quería demostrar.

Bisectriz
de un ángulo Se llama
bisectriz de un ángulo a la semirrecta que divide a un ángulo
en dos ángulos iguales. Por lo tanto, la bisectriz de un ángulo
es el lugar geométrico de los puntos que equidistan de los lados del ángulo. 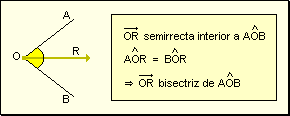
Mediatriz
de un segmento Se llama mediatriz
de un segmento a la recta perpendicular que lo divide en dos segmentos iguales.
Por lo tanto, la mediatriz de un segmento es el lugar geométrico de los
puntos que equidistan de los extremos del segmento. 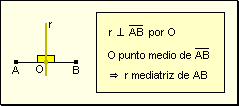

Definición
de circunferencia El conjunto
de puntos del plano que cuya distancia respecto de un punto O es igual al segmento
r se llama circunferencia. Por lo tanto la circunferencia es el lugar geométrico
de los puntos que equidistan de un punto fijo. 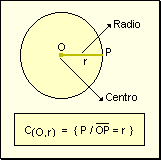
Dada
una circunferencia pueden definirse diferentes posiciones relativas entre:
w Un
punto y una circunferencia w
Una recta y una circunferencia w
Dos circunferencias entre
sí 
Posiciones
relativas entre un punto y una circunferencia Los
puntos del plano al que pertenece la circunferencia pueden ser:
w Interiores:
Un punto es interior a una circunferencia si su distancia al centro es menor que
el radio. 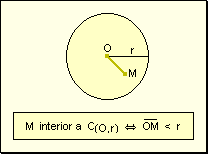
w De
la circunferencia: Un punto pertenece a la circunferencia si su distancia
al centro es igual al radio. 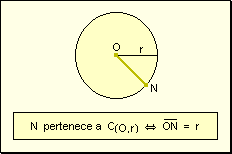
w Exteriores:
Un punto es exterior a una circunferencia si su distancia al centro es mayor que
el radio. 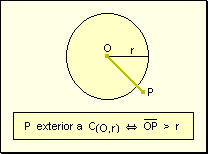

Posiciones
relativas entre una recta y una circunferencia Una
recta incluida en el plano al que pertenece la circunferencia puede ser:
w Exterior:
Una recta es exterior a una circunferencia cuando la intersección con la
misma es nula. 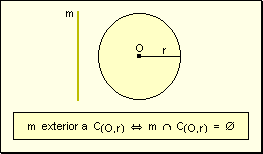
w Tangente:
Una recta es tangente a una circunferencia cuando comparten un único punto. 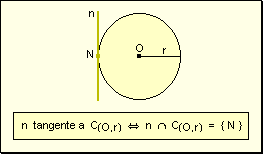
w Secante:
Una recta es secante a una circunferencia cuando la corta en dos puntos. 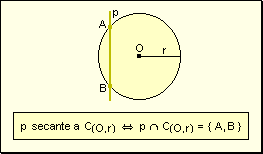

Posiciones
relativas de dos circunferencias Una
circunferencia perteneciente al mismo plano al que pertenece una segunda circunferencia
puede ser: w
Exterior: Una circunferencia es exterior a otra si y sólo si la
distancia de los centros es mayor que la suma de los radios. 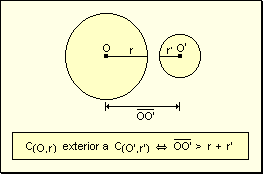
w Tangente
exterior: Una circunferencia es tangente exterior a otra si y sólo
si la distancia de los centros es igual a la suma de los radios. 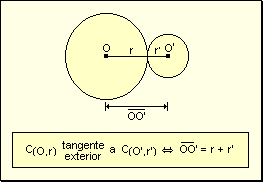
w Secante:
Una circunferencia es secante a otra si y sólo si la distancia de los centros
es menor a la suma de los radios. 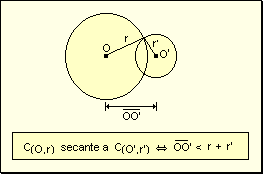
w Tangente
interior: Una circunferencia es tangente interior a otra si y sólo
si la distancia de los centros es igual a la diferencia de los radios. 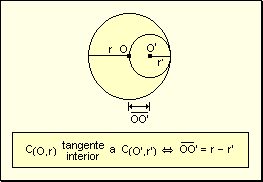
w Interior:
Una circunferencia es interior a otra si y sólo si la distancia de los
centros es menor a la diferencia de los radios. 
w Concéntrica:
Una circunferencia es concéntrica a otra si y sólo si la distancia
de los centros es nula, o sea que sus centros coinciden. 
| 
