| 
Rectas
perpendiculares Dos
rectas son perpendiculares cuando al cortarse
forman cuatro ángulos iguales. 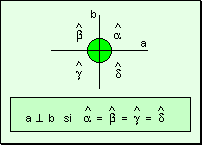
Dado
un punto perteneciente a una recta o exterior a ella, por él pasa una y
sólo una perpendicular a dicha recta. 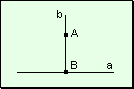
El
trazado de perpendiculares
puede efectuarse de las siguientes formas:
w Con
escuadra, por un punto perteneciente a la recta o exterior a la misma. w
Con compás, por un punto perteneciente a la recta o exterior a la
misma. Rectas paralelas Dos
rectas son paralelas
cuando no tienen ningún punto en común, o cuando son coincidentes. 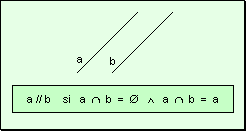
Dado
un punto perteneciente a una recta o exterior a ella, por él pasa una y
sólo una paralela a dicha recta. 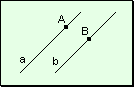
El
trazado de paralelas
puede efectuarse de las siguientes formas:
w Con
regla y escuadra w
Con regla y compás
Teorema:
En un plano, dos rectas perpendiculares
a una tercera son paralelas.

Propiedades
de la perpendicularidad
w Carácter
reflexivo: La perpendicularidad no cumple con el carácter reflexivo. 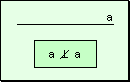
w Carácter
simétrico: Si una recta es perpendicular a otra, ésta es perpendicular
a la primera. 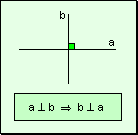
w Carácter
transitivo: La perpendicularidad no cumple con el carácter transitivo. 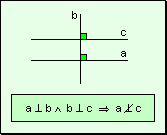

Propiedades
del paralelismo
w Carácter
reflexivo: Toda recta es paralela a si misma. 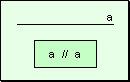
w Carácter
simétrico: Si una recta es paralela a otra, ésta es paralela
a la primera. 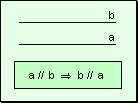
w Carácter
transitivo: Si una recta es paralela a otra y ésta es paralela a una
tercera, la primera recta es paralela a la tercera. 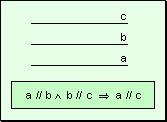

Teorema En
un plano, dos rectas perpendiculares a una tercera son paralelas. 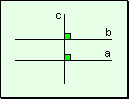
Hipótesis 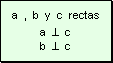
Tesis 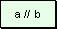
Demostración (por
el método del absurdo) Si a
no fuera paralela a b , las rectas se cortarían en un punto R. 
Por
hipótesis, por el punto R pasarían dos rectas perpendiculares
a la recta c. 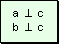
y
ésto es absurdo ya que por un punto exterior a una recta pasa una
y sólo una perpendicular a la misma.
 Angulos
determinados por dos rectas paralelas cortadas
por una transversal Dos rectas
cualesquiera cortadas por una tercera determinan ocho ángulos. 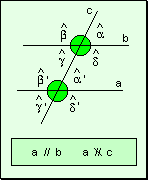
De
acuerdo a la ubicación
de los mismos se clasifican en:
w Angulos
interiores y exteriores w
Angulos correspondientes w
Angulos alternos w
Angulos conjugados

Angulos
interiores Los ángulos
ubicados en la zona comprendida entre las rectas paralelas se llaman ángulos
interiores. 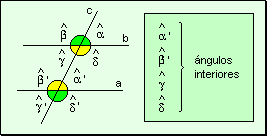
Angulos
exteriores Los ángulos
que no son interiores se denominan ángulos exteriores. 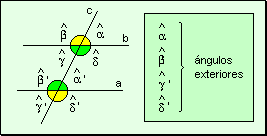

Angulos
correspondientes Si dos ángulos
están ubicados de un mismo lado de la transversal, uno es interior y el
otro es exterior, se los llama ángulos correspondientes. 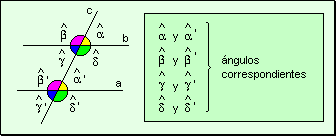
Los
ángulos correspondientes entre paralelas son iguales. Recíprocamente,
si dos rectas cortadas por una tercera forman ángulos correspondientes
iguales, las rectas son paralelas. 
Angulos
alternos internos Si dos ángulos
están situados en distintos semiplanos con respecto a la transversal y
ambos son internos, se los llama ángulos alternos internos. 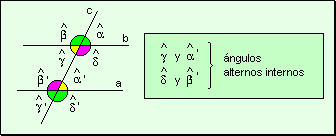
Los
ángulos alternos internos entre paralelas son iguales. Recíprocamente,
si dos rectas cortadas por una tercera forman ángulos alternos internos
iguales, las rectas son paralelas. Angulos
alternos externos Si dos ángulos
están situados en distintos semiplanos con respecto a la transversal y
ambos son externos, se los llama ángulos alternos externos. 
Los
ángulos alternos internos entre paralelas son iguales. Recíprocamente,
si dos rectas cortadas por una tercera forman ángulos alternos externos
iguales, las rectas son paralelas. 
Angulos
conjugados internos Si dos ángulos
están situados en un mismo semiplano con respecto a la transversal y ambos
son internos, se los llama ángulos conjugados internos. 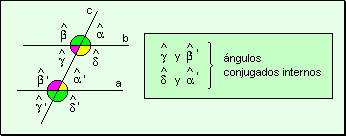
Los
ángulos conjugados internos entre paralelas son suplementarios. Recíprocamente,
si dos rectas cortadas por una tercera forman ángulos conjugados internos
suplementarios, las rectas son paralelas. Angulos
conjugados externos Si dos ángulos
están situados en un mismo semiplano con respecto a la transversal y ambos
son externos, se los llama ángulos conjugados externos. 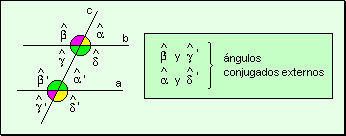
Los
ángulos conjugados internos entre paralelas son suplementarios. Recíprocamente,
si dos rectas cortadas por una tercera forman ángulos conjugados internos
suplementarios, las rectas son paralelas.
| 
