| 
Definición
1 Dados
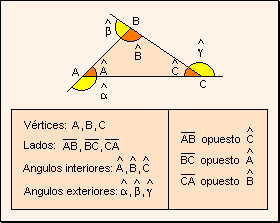
en un plano tres puntos A, B y C no alineados, se llama triángulo 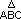 a la intersección de los ángulos convexos
a la intersección de los ángulos convexos 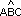 ,
, 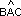 y y  . . 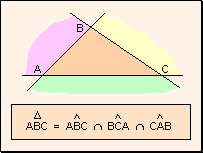
Definición
2 Dados
en un plano tres puntos A, B y C no alineados, se llama triángulo 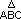 a la intersección del semiplano de borde
a la intersección del semiplano de borde 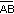 que contiene al punto C, el semiplano
que contiene al punto C, el semiplano 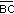 que contiene al punto A y el semiplano
que contiene al punto A y el semiplano 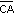 que contiene al punto B.
que contiene al punto B. 

Según
sus lados w
Equilátero: tres lados iguales w
Isósceles: dos lados iguales. w
Escaleno: tres lados desiguales. 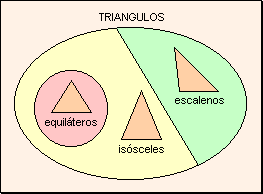
Según
sus ángulos w
Acutángulo: tres ángulos agudos w
Rectángulo: un ángulo recto w
Obtusángulo: un ángulo obtuso 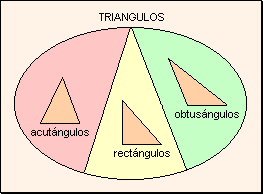

Igualdad
de triángulos Dos triángulos
son congruentes cuando tienen todos sus lados y ángulos respectivamente
congruentes. 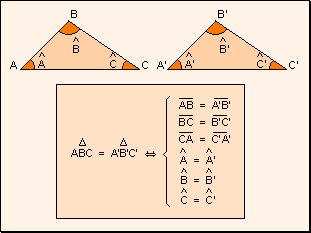
Sólo
es necesario verificar que ciertos elementos sean congruentes para que dos triángulos
sean iguales, por lo que se definen 4
criterios de igualdad de triángulos.
A partir de los criterios de igualdad anteriores derivan los criterios de igualdad
de triángulos rectángulos.
La igualdad de triángulos cumple las propiedades
reflexiva, simétrica
y transitiva. 
Propiedades
de la igualdad de triángulos
w
Carácter reflexivo: Todo triángulo es igual a si mismo. 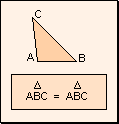
w Carácter
simétrico: Si un triángulo es igual a otro, éste es igual
a primero. 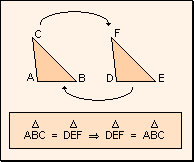
w Carácter
transitivo: Si un triángulo es igual a otro y éste es igual
a un tercero, el primero es igual al tercero. 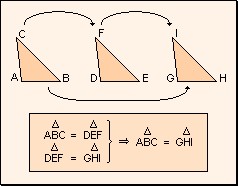

Criterios
de igualdad de triángulos
w Primer
criterio: Dos triángulos que tienen dos lados y el ángulo comprendido
respectivamente iguales, son iguales. 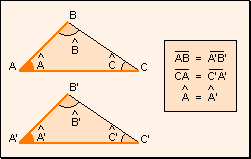
w Segundo
criterio: Dos triángulos que tienen dos ángulos y un lado respectivamente
iguales, son iguales. 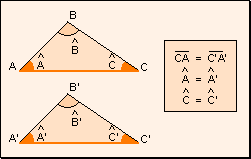
w Tercer
criterio: Dos triángulos que tienen sus tres lados respectivamente
iguales, son iguales. 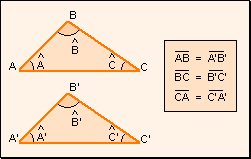
w Cuarto
criterio: Dos triángulos que tienen dos lados y el ángulo opuesto
al lado mayor respectivamente iguales, son iguales. 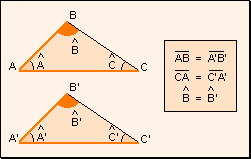

Criterios
de igualdad de triángulos rectángulos
w Primer
criterio: Dos triángulos rectángulos que tienen sus catetos
respectivamente iguales, son iguales. 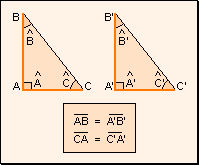
w Segundo
criterio: Dos triángulos rectángulos que tienen un ángulo
agudo y un cateto respectivamente iguales, son iguales. 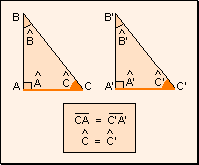
w Tercer
criterio: Dos triángulos que tienen un cateto y la hipotenusa respectivamente
iguales, son iguales. 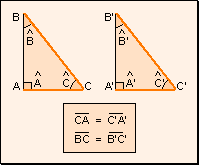
w Cuarto
criterio: Dos triángulos rectángulos que tienen un ángulo
agudo y la hipotenusa respectivamente iguales, son iguales. 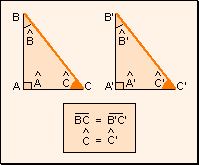

Propiedad
de la suma de los ángulos interiores de un triángulo Teorema: La
suma de los ángulos interiores de un triángulo es igual a 180º. Disponiendo
los ángulos del triángulo en forma consecutiva se obtiene un ángulo
llano. 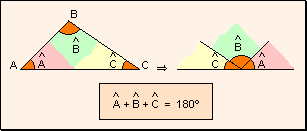
Corolarios:
w En
todo triángulo, cada ángulo es igual a 180º menos la suma de los
otros dos ángulos. w
Si en un triángulo un ángulo es rectángulo u obtuso, los
dos ángulos restantes son agudos. w
Si dos triángulos tienen dos ángulos iguales, los terceros también
son iguales. Propiedad
del ángulo exterior Teorema: Todo
ángulo exterior de un triángulo es igual a la suma de los dos ángulos
interiores no adyacentes. 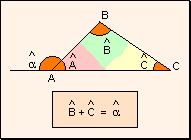
Corolario:
w En
todo triángulo, cada ángulo exterior es mayor que cualquiera de
los ángulos interiores. 
Teorema
de los ángulos interiores Hipótesis 
Tesis 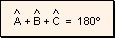
Demostración Se
traza por C una recta paralela al lado 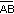 , quedando determinados los ángulos
, quedando determinados los ángulos  y
y 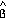 . . 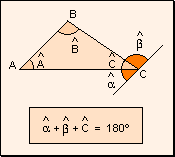
De
lo anterior: 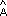 =
=  por ser alternos
internos entre r // AB y secante por ser alternos
internos entre r // AB y secante 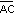
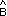 =
= 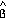 por ser alternos
internos entre r // AB y secante por ser alternos
internos entre r // AB y secante 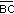
Por
lo tanto: 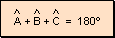
que
es lo que se quería demostrar.
| 
