| 
Definición Se
llama producto de un ángulo por un número natural n al ángulo
formado suma de por n ángulos iguales al dado. 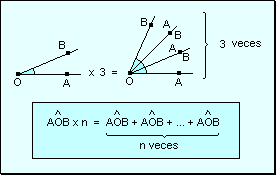
La multiplicación
de un ángulo por un número natural es
ley
de composición externa. La
multiplicación de un ángulo por un número natural cumple
con las siguientes leyes y propiedades:
w Existencia
de elemento neutro y absorvente w
Ley asociativa w
Propiedad distributiva 
Elemento
neutro El número 1
es el elemento neutro del producto entre un ángulo y un número natural:
el producto de cualquier ángulo por 1 es el mismo ángulo. 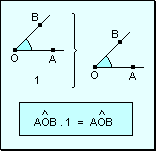
Elemento
absorbente El número 0
es el elemento absorbente del producto entre un ángulo y un número
natural: el producto de cualquier ángulo por 0 es igual al ángulo
nulo. 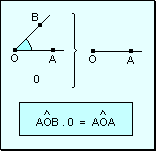

Ley
asociativa El producto de un
ángulo por varios números naturales es asociativo, ya que no depende
de la forma que se asocien los factores: si se reemplazan dos factores por su
producto efectuado, el resultado no varía. 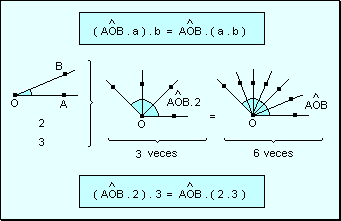
 Propiedad
distributiva w
El producto de una suma de ángulos por un número natural es igual
a la suma de los productos de cada ángulo por ese número natural. 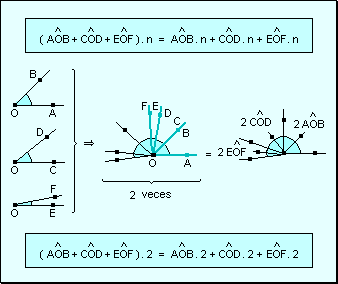
w El
producto de un ángulo por la suma de números naturales es igual
a la suma de los productos del ángulo por cada número natural. 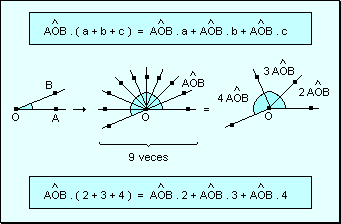

Ley
de composición externa Se
llama ley de composición externa a las operaciones definidas entre
elementos de distintos conjuntos. La
multiplicación y división de un ángulo por un número
natural es ley de composición externa. 

Definición Se
llama cociente de un ángulo por un número natural n distinto de
cero, a otro ángulo tal que multiplicado por el número de como resultado
el ángulo original. 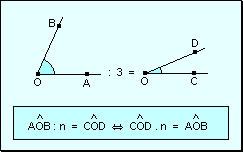
La división de un ángulo por
un número natural es
ley
de composición externa. La
división de un ángulo por un número natural cumple con las
siguientes leyes y propiedades:
w Corolarios w
Existencia del elemento neutro w
Propiedad distributiva 
Corolarios
w Si
a un ángulo se lo multiplica por un número natural y al ángulo
resultante se lo divide por el mismo número, se obtiene un ángulo
igual al original. 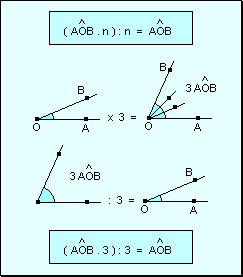
w Si
a un ángulo se lo divide por un número natural y al ángulo
resultante multiplica por el mismo número, se obtiene un ángulo
igual al original. 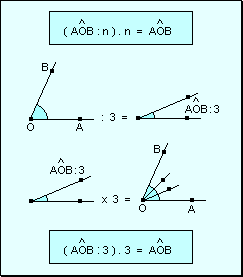

Elemento
neutro El número uno es
el elemento neutro de la división de ángulos por un número
natural. 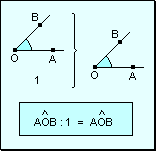

Propiedad
distributiva La división
de una suma de ángulos por un número natural es igual a la suma
de los cocientes de cada ángulo por ese número natural. 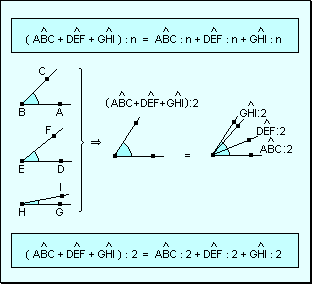

Ley
de composición externa Se
llama ley de composición externa a las operaciones definidas entre
elementos de distintos conjuntos. La
multiplicación y división de un ángulo por un número
natural es ley de composición externa. 

Angulos
convexos Un ángulo convexo
es aquel en el cual, al trazar un segmento uniendo dos puntos cualesquiera de
sus lados, el segmento se encontrará dentro del ángulo. 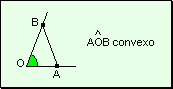
Los
ángulos convexos se clasifican en:
w Agudos w
Rectos w
Obtusos w
Llanos Angulos
cóncavos Un ángulo
cóncavo es aquel en el cual, al trazar un segmento uniendo dos puntos cualesquiera
de sus lados, el segmento se encontrará fuera del ángulo. 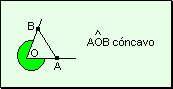
Los
ángulos cóncavos son mayores que un llano.

Angulos
rectos Un ángulo recto
es aquel formado por el cruce de dos rectas perpendiculares. 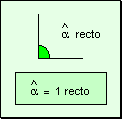
Todos
los ángulos rectos son iguales. 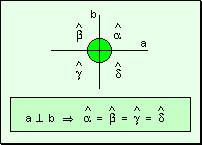

Angulos
llanos Un ángulo llano
es aquel cuyos lados son semirrectas opuestas. 
Todo
ángulo llano es igual a dos rectos. 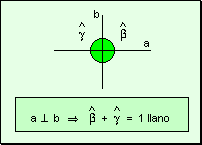

Angulos
agudos Un ángulo agudo
tiene una abertura menor a la del ángulo recto. 

Angulos
obtusos Un ángulo obtuso
tiene una abertura mayor a la del ángulo recto. 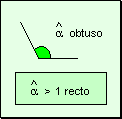

Unidades
angulares La unidad de medida de
los ángulos se llama grado, y resulta de dividir un ángulo
recto en 90 partes iguales, por lo tanto, un ángulo
recto mide 90º. 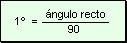
Por
lo tanto: w
Angulo agudo < 90º w
Angulo recto
= 90º w
Angulo obtuso > 90º y < 180º w
Angulo llano
= 180º w
Angulo cóncavo >
180º El sistema de medición
de los ángulos se llama sexagesimal. Recibe este nombre porque cada unidad
menor al grado se divide en 60 partes para obtener la siguiente: 

Angulos
complementarios Dos ángulos
son complementarios cuando la suma de sus amplitudes da como resultado un recto. 

Angulos
adyacentes Dos ángulos
son adyacentes cuando tienen un lado en común y el otro lado está
formado por dos semirrectas opuestas. 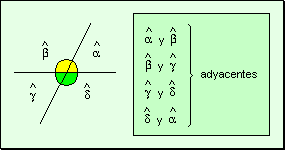
w Los
ángulos adyacentes son siempre suplementarios,
ya que su suma es igual a un llano. w
Si dos ángulos adyacentes son iguales, ambos son ángulos rectos. Angulos
opuestos por el vértice Dos
ángulos son opuestos por el vértice cuando tienen un vértice
en común y sus lados son semirrectas opuestas. 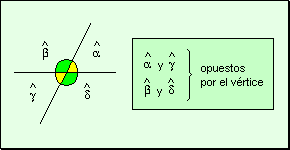
Teorema:
Los ángulos opuestos por el vértice son iguales.

Angulos
suplementarios Dos ángulos
son suplementarios cuando la suma de sus amplitudes da como resultado un llano. 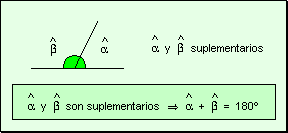

Teorema Los
ángulos opuestos por el vértice son iguales. 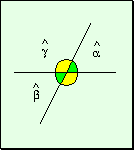
Hipótesis 
Tesis 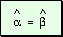
Demostración Considerando
el ángulo 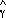 adyacente a
adyacente a  : : 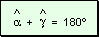
Como
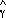 es también
adyacente a es también
adyacente a 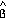 : : 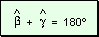
Como
dos ángulos que tienen igual suplemento son iguales,  y
y 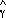 resultan iguales. resultan iguales. 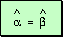
que
es lo que se quería demostrar.
| 
