| 
Definición Toda
recta perteneciente a un plano separa al mismo en dos porciones, cada uno de ellos
recibe el nombre de semiplano.
A la recta que da lugar a los dos semiplanos se la llama frontera o recta de división.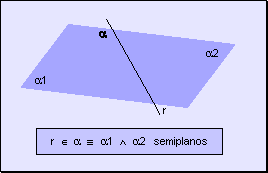 
Para
diferenciar los semiplanos se determinan dos puntos adicionales, cada uno de los
cuales pertenece a cada semiplano:
w Semiplano
respecto a la recta r que contiene al punto A w
Semiplano respecto a la recta r que contiene al punto B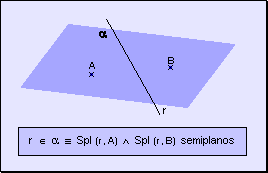 
Propiedades
de los semiplanos Se observa
que: w
La intersección de dos semiplanos determinados por una recta es la recta
de división.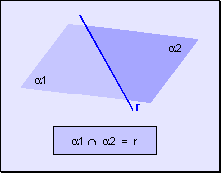 
w La
unión de dos semiplanos determinados por una recta es todo el plano.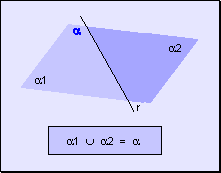 
w Todo
punto de un plano pertenece a uno de los dos semiplanos o a la recta de división.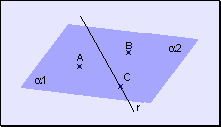 
w Todo
segmento determinado por dos puntos de distintos semiplanos corta a la recta de
división.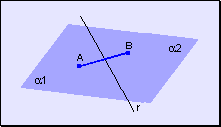 
w Todo
segmento determinado por dos puntos del mismo semiplano no corta a la recta de
división.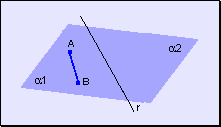 
Definición Cuando
dos rectas se cortan, forman en el plano 4 regiones llamadas ángulos.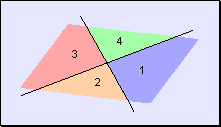 
Dados
dos planos se llama ángulo convexo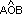 
a la intersección del semiplano respecto de la recta 
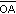que contiene al punto B y el semiplano respecto a la recta 
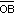que contiene al punto A.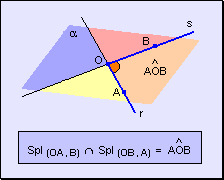 
Si
en cambio, se considera la unión de los dos semiplanos queda determinado
un ángulo cóncavo. Si se suprime un ángulo convexo
del plano, lo que queda es un ángulo cóncavo.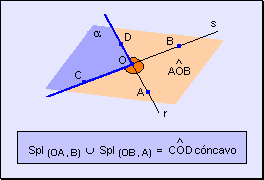 
Las
relaciones angulares verifican las siguientes propiedades:
w Igualdad
de ángulos: se verifican las leyes
reflexiva, simétrica y transitiva. w
Relación de orden de
ángulos: forman un conjunto ordenado.
Identificación
de un ángulo Por lo tanto,
un ángulo es la porción de plano delimitado por dos semirrectas
del mismo origen, y está delimitado por:
w Un
vértice: punto de origen de las dos semirrectas que lo forman. w
Dos lados: semirrectas cuyo origen forma el vértice del ángulo.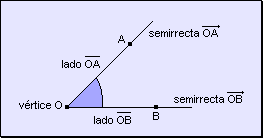 
Los
ángulos se identifican por tres letras donde:
· La letra
central corresponde al vértice. ·
Las otras dos letras son puntos cualesquiera de las semirrectas que lo forman.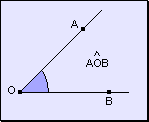 
Cuando
los lados del ángulo son dos semirrectas opuestas se denomina ángulo
llano. El ángulo llano a un semiplano. 
Punto
interior a un ángulo Todo
punto perteneciente a un ángulo que no pertenece a sus lados se llama punto
interior al ángulo.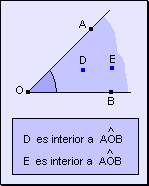 
Semirrecta
interior a un ángulo Toda
semirrecta cuyo origen coincide con el vértice del ángulo y sus
demás puntos son interiores al ángulo se llama semirrecta interior
al ángulo.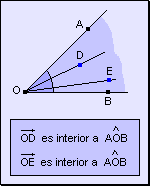 
Segmento
y ángulo Si un segmento
tiene sus extremos en los lados de un ángulo, toda semirrecta interior
a ese ángulo corta al segmento en un punto interior al ángulo.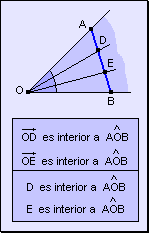 
Igualdad
de ángulos Dos ángulos
son congruentes cuando tienen la misma amplitud. Al colocar uno encima
del otro haciendo coincidir el vértice y uno de sus lados, el otro lado
coincide. w
Carácter reflexivo: todo ángulo es igual a si mismo.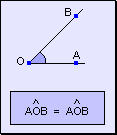 
w Carácter
simétrico: Si un ángulo es igual a otro, éste es igual
al primero.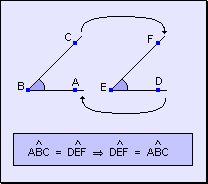 
w Carácter
transitivo: Si un ángulo es igual a otro y éste es igual a un
tercero, el primer ángulo es igual al tercero.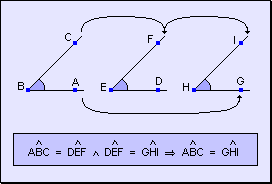 
Relación
de orden de ángulos
w Si un ángulo
es mayor que otro y éste es mayor que un tercero, el primer ángulo
es mayor que el tercero.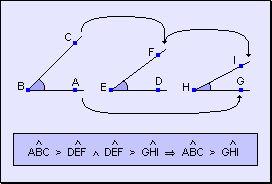 
w Si
un ángulo es mayor que otro y éste es igual a un tercero, el primer
ángulo es mayor que el tercero.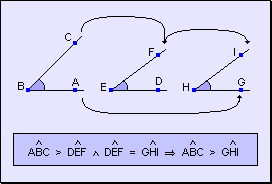 
w Si
un ángulo es igual a otro y éste es mayor que un tercero, el primer
ángulo es mayor que el tercero.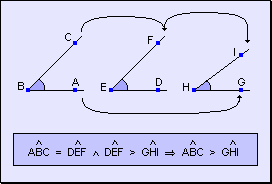 
Postulado
de las tres posibilidades Dados
dos ángulos, debe verificarse una y sólo una de las siguientes tres
posibilidades: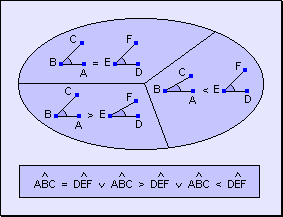 
| 
