| 
Definición Se
define como segmentos consecutivos a aquellos que cumplen las siguientes propiedades:
w Dos segmentos
son consecutivos cuando tienen un extremo en común. w
Varios segmentos son consecutivos cuando cada uno es consecutuvo sólamente
con el anterior y con el siguiente. 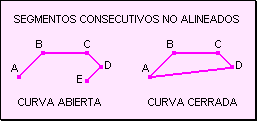
w Si
los segmentos consecutivos pertenecen a una misma recta son consecutivos alineados:
tienen un extremo en común y los puntos restantes pertenecen a semirrectas
opuestas. 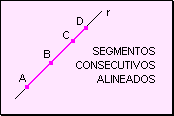

Definición La
suma de segmentos consecutivos alineados es igual al segmento formado por los
extremos no comunes de los segmentos (la unión de los puntos de ambos segmentos). 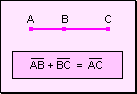
La adición de segmentos
es
ley de composición
interna. Para
sumar dos segmentos, éstos deben ser consecutivos. Si los segmentos no
son consecutivos, deben colocarse sobre una recta segmentos congruentes a los
dados en forma consecutiva alineada. 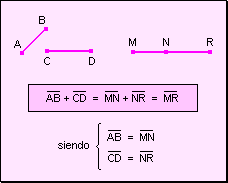
La
adición de segmentos cumple con las siguientes leyes y propiedades:
w Ley
de cierre y uniforme w
Ley conmutativa y asociativa w
Existencia del elemento neutro 
Ley
de cierre La suma de dos segmentos
es cerrada o completa ya que su resultado es siempre un segmento. 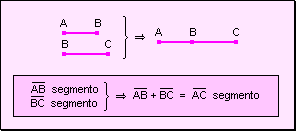
Ley uniforme La
adición de segmentos es uniforme ya que su resultado es único. Si
a ambos miembros de una igualdad se le suma un mismo segmento se obtiene otra
igualdad. 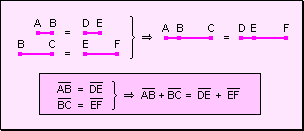
| 
