| 
Conceptos
fundamentales La
geometría se basa en tres conceptos fundamentales
que se aceptan sin definirlos y que forman parte
del espacio geométrico, o sea el conjunto formado por todos los
puntos: w
El punto: Un punto se representa con una pequeña cruz y se lo designa
con una letra de imprenta mayúscula. 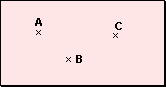
w La
recta: Una recta se representa con una porción de la misma y se la
designa con una letra de imprenta minúscula. 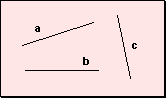
w El
plano: Un plano se representa con una porción del mismo y se lo designa
con una letra griega. 

Relaciones
fundamentales Los tres conceptos
anteriores están relacionados a través de las relaciones de pertenencia
e inclusión: w
Los puntos pertenecen a las rectas y los planos. 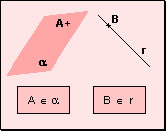
w Las
rectas están incluidas en los planos. 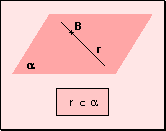

Postulados Se
llaman postulados a aquellas propiedades que satisfacen los elementos geométricos
que se aceptan sin demostrar y que surgen de la simple observación.
1. Existen infinitos puntos, infinitas rectas e
infinitos planos. 
2. Todo punto pertenece a infinitas rectas, ya
que por un punto pasan infinitas rectas. 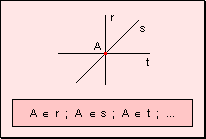
El conjunto de rectas que concurren en un punto
se denomina haz de rectas. 3. Toda recta
está incluida en infinitos planos ya que por una recta pasan infinitos
planos. 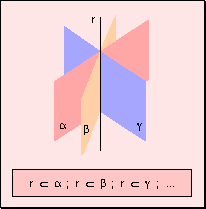
El conjunto de planos que pasa por una recta se
denomina haz de planos. 4. Dos puntos
determinan una y sólo una recta a la cual pertenecen. 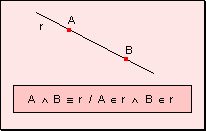
5. A una recta pertenecen infinitos puntos y existen
también infinitos puntos que no pertenecen a ella. 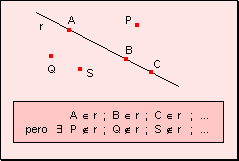
6. Una recta y un punto fuera de ella determinan
un plano de modo que el punto pertenece al mismo y la recta está incluida
en él. 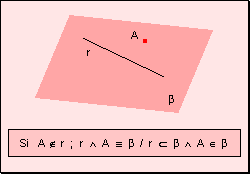
7. La recta determinada por dos puntos de un plano
está incluida a dicho plano. 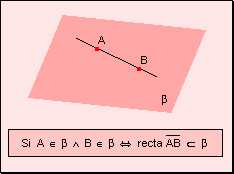
También puede enunciarse como: Dos puntos
incluidos en un plano determinan una recta que está incluida en el plano. 8.
A un plano pertenecen infinitos puntos y existen también infinitos puntos
que no pertenecen a ella. 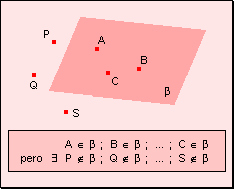

Definición Todo
punto perteneciente a una recta separa a la misma en dos porciones, cada una de
ellas recibe el nombre de semirrecta.
Al punto que da lugar a las dos semirrectas opuestas se lo llama origen. Para
diferenciar las semirrectas se determinan dos puntos adicionales, cada uno de
los cuales pertenece a cada semirrecta:
w Semirrecta
de origen O que pasa por el punto A w
Semirrecta de origen O que pasa por el punto B 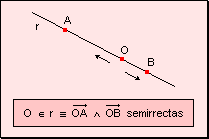

Características
de las semirrectas w
Todo punto de una recta pertenece a una de las dos semirrectas o coincide con
el origen. w
La intersección de dos semirrectas opuestas es el punto de origen. 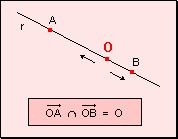
w La
unión de dos semirrectas opuestas es toda la recta. 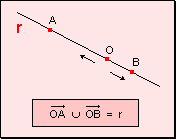

Definición Dados
dos puntos A y B, se llama segmento a la intersección de la semirrecta
de origen A que contiene al punto B y la semirrecta de origen B que contiene al
punto A. Los puntos A y B se denominan
extremos del segmento. 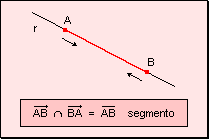
Se
observa que: w
Dos puntos pertenecientes a una misma semirrecta determinan un segmento que no
contiene al origen. 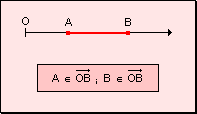
w Dos
puntos pertenecientes a distintas semirrectas determinan un segmento que contiene
al origen. 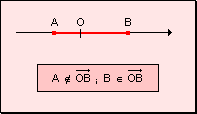
Se
verifican las siguientes propiedades:
w Igualdad
de segmentos: se verifican las leyes reflexiva,
simétrica y transitiva. w
Relación de orden de
segmentos: forman un conjunto ordenado.

Igualdad
de segmentos w
Carácter reflexivo: todo segmento es igual a si mismo. 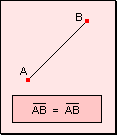
w Carácter
simétrico: Si un segmento es igual a otro, éste es igual al
primero. 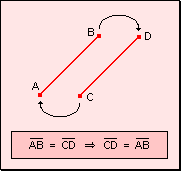
w Carácter
transitivo: Si un segmento es igual a otro y éste es igual a un tercero,
el primer segmento es igual al tercero. 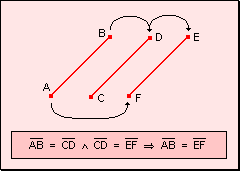

Relación
de orden w
Si un segmento es mayor que otro y éste es mayor que un tercero, el primer
segmento es mayor que el tercero. 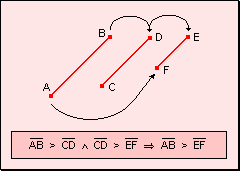
w Si
un segmento es mayor que otro y éste es igual a un tercero, el primer segmento
es mayor que el tercero. 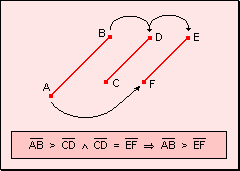
w Si
un segmento es igual a otro y éste es mayor que un tercero, el primer segmento
es mayor que el tercero. 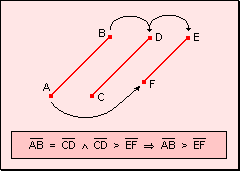
Postulado
de las tres posibilidades Dados
dos segmentos, debe verificarse una y sólo una de las siguientes tres posibilidades: 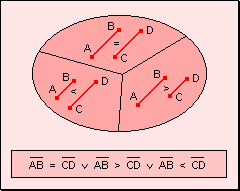
| 
