Definición

El producto de los cardinales de dos conjuntos A y B es igual al cardinal del producto cartesiano A x B.

En el caso del producto no es necesario que los conjuntos sean disjuntos, como en la suma. Por lo tanto, el producto de dos números a y b es igual al número s de elementos del conjunto formado por los pares ordenados del producto cartesiano A x B.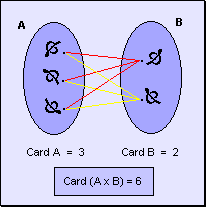

A partir de la definición anterior podemos decir que el producto de dos números naturales es una función que a todo par ordenado de números naturales le hace corresponder otro número natural llamado producto. Este número será múltiplo de cada uno de los factores. Por lo tanto, el producto es una operación binaria, ya que puede realizarse únicamente entre dos elementos.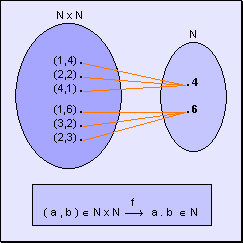

También puede interpretarse como una suma repetida: el producto de dos números naturales a . b puede definirse como la suma de b sumandos iguales a a.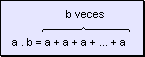

El producto como operación binaria

El producto es una operación binaria, ya que puede realizarse únicamente entre dos elementos.

Para multiplicar más de dos números, se multiplican los dos primeros factores, al resultado se le multiplica el tercer factor y así sucesivamente.

Producto de dos sumas

En el caso en que los dos elementos a multiplicar sean sumas algebraicas se procede siguiendo la siguiente regla:

El producto de una suma por otra es igual a la suma de los productos que se obtienen multiplicando cada término de la primera suma por cada miembro de la segunda suma.

Conjuntos disjuntos

Si los conjuntos no fueran disjuntos: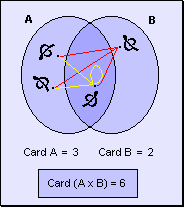

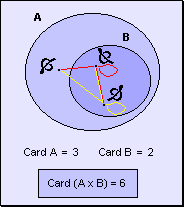
Se observa que el resultado no cambia.

a