|
Regla de los signos de
la radicación
w
Toda raíz de índice impar conserva el signo del radicando. 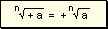
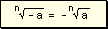
w Toda
raíz de índice par y radicando positivo da como resultado dos números
opuestos. 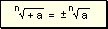
w La
raíz de índice par y radicando negativo es imposible de resolver
en el conjunto de números enteros. 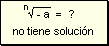
Números racionales Ante
la imposibilidad de efectuar una división cuando el dividendo no es múltiplo
del divisor se crea el conjunto de números fraccionarios puros,
que se representan como: 
y
expresa la división del número a por el número b,
donde a no es múltiplo de b. Estos números a
y b pueden ser positivos o negativos, por lo que el signo
de la fracción depende del signo del
numerador y el denominador. Uniendo este
nuevo conjunto al conjunto de números enteros obtendremos el conjunto de
números racionales,
que se define: 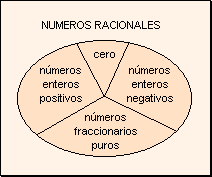
Representación
gráfica de números racionales 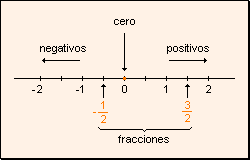
El
conjunto de números racionales se designa con la letra Q. A partir
de su representación gráfica se observa que:
w El
conjunto de números racionales no tiene ni primer ni último elemento. w
Todo número racional tiene un antecesor y un sucesor. w
Entre dos números racionales existen infinitos números racionales,
por lo que el conjunto es denso. 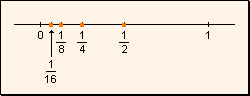
Signo de una fracción El
signo de una fracción es el que resulta de aplicar la regla de los signos
de la división de números enteros. 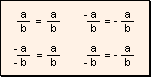
Por
convención, el signo se escribe delante de la raya de la fracción. a
| 
