|
Ley
de cierre La
división de dos números naturales no es cerrada o completa
ya que su resultado es un número natural si y sólo si el dividendo
es múltiplo del divisor y el divisor es distinto de cero. 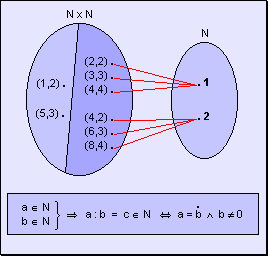
Ley conmutativa La
división de números naturales no es conmutativa, ya que depende
del orden entre dividendo y divisor: al cambiar el orden de los mismos el cociente
varía. 
Ley
asociativa La división
de números naturales no es asociativa, ya que depende de la forma
que se asocien los operandos: si se reemplazan dos operandos por su división
efectuada, el cociente final varía. 
Producto Algebraico
- Definición Se llama
producto algebraico a la combinación de multiplicaciones y divisiones de
números naturales. Para resolver un producto algebraico se procede de alguna
de las siguientes formas: w
Realizando las operaciones de a dos números en el orden en que aparecen. 
w Dividiendo
del producto de los números que figuran multiplicando, el producto de los
números que figuran dividiendo. 
Como
caso especial puede destacarse la resolución del producto
de divisiones.
Nótese que no estamos hablando
de términos sino de números. Si
en un producto algebraico aparecen paréntesis,
corchetes y llaves, para resolver el mismo
se resuelven, en primer lugar las operaciones que figuran entre paréntesis,
luego las que aparecen entre corchetes
y por último las que están entre llaves,
en ese orden. Simplificación De
acuerdo a los corolarios de la división: 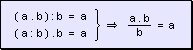
Por
lo tanto, cuando en un producto algebraico un mismo número figura multiplicando
y dividiendo, éste puede simplificarse.
Uso
de paréntesis, corchetes y llaves
Cuando
en una operación aparece entre paréntesis, corchetes o llaves, se
está indicando el número resultado de esa operación. Estos
símbolos se utilizan para remarcar el orden de resolución del producto
algebraico.
Supresión
de paréntesis
w Los paréntesis,
corchetes o llaves precedidos por el operador por, pueden suprimirse, conservando
las operaciones de los valores que encerraba, o sea que mantienen los
mismos operadores. 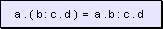
w Los
paréntesis, corchetes o llaves precedidos por el operador dividido,
pueden suprimirse, invirtiendo las operaciones de los valores que encerraba,
o sea que cambian sus operadores anteriores por los operadores contrarios. 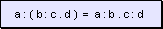
Intercalación de paréntesis
w Si
se desean intercalar paréntesis precedidos por el operador por,
los valores que encierran conservan las operaciones, o sea que mantienen
los mismos operadores. 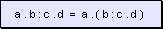
w Si
se intercalan paréntesis precedidos por el operador menos, los valores
que encierran invierten las operaciones, o sea que cambian sus operadores
anteriores por los operadores contrarios. 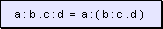
| 
